1. The mathimatical defintiion of an ellipse is "the set of all points such that the sum of the distance from two points is a constant."
2. The first way to descibe an ellipse is algebraically. The equation of an ellipse looks something like this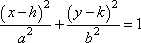 
. From this information we will be able to find the center of the graph which is always (h, k). To find the vertices and co-vertices from the equation we must find a nd b. We find a and b from the equation, all we need to do is sqaure root a^2 and b^2. By finding a we know how far each vertices are away from the center. By finding B we know how far each co-vertices are from the center. To find c we need to use a^2-b^2=c^2. After sqaure rooting that answer we now have found c agebrically and we know how far away the 2 foci are from the center. Lastly if the major axis is vertical we know a, which is the bigger number will be under y^2. If the major axis is horizontalm a will be under x^2.
. From this information we will be able to find the center of the graph which is always (h, k). To find the vertices and co-vertices from the equation we must find a nd b. We find a and b from the equation, all we need to do is sqaure root a^2 and b^2. By finding a we know how far each vertices are away from the center. By finding B we know how far each co-vertices are from the center. To find c we need to use a^2-b^2=c^2. After sqaure rooting that answer we now have found c agebrically and we know how far away the 2 foci are from the center. Lastly if the major axis is vertical we know a, which is the bigger number will be under y^2. If the major axis is horizontalm a will be under x^2.
Another way to describe an ellipse is graphically. First we find the center of the ellipse by just looking at the equation. After that we can identify the major axis by looking at the x^2 and y^2. If a is under the x^2 then it is horinzontal. If a is under the y^2 then it is vertical. Next we find a and b to be able to find the vertices and co-vertices. For plotting the vertices we move a times to the left and right if a is under the x^2 and a units up and down if it is under the y^2. For plotting the co-vertices we got b units up and down if b under y^2 and goes left and right when it is under x^2. If the foci of the ellipse are closer to the center, the ellipse will become more ciruclar. If it is farther away from the center, then it will become less circular. We find the eccentricity of an ellipse by doing c/a and it has to be between 0 and 1.
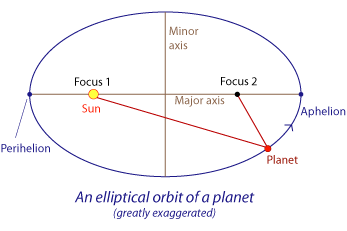
3. The real life application I found for ellipse's are the oribits of the planets in our solar system. The orbits of the plants are ellipses because "the Sun is one focus of the ellipse."(http://csep10.phys.utk.edu/astr161/lect/history/kepler.html). So according to this website, the sun is one of the two foci in an ellipse. The other focus is probably another planet. Scientist usually say planets have an eccentric orbit. When they say eccentric orbit they mean far from being circular. So pluto, even though it is not a planet anymore, still oribits around eccentrically.
Another thing i found out that the planets are the vertices and co vertices. I say this because the planets are the objects going around like an ellipse so they are the ones touching the ellipse. If a planet is orbiting farther away, then it is on the major axis. It is on the major axis because that is the bigger axis. Once it is rotating and it closer to the center, then it is on the minor axis. It is on the minor axis because it got closer from the major axis.
4. Work Cited:
- http://www.purplemath.com/modules/ellipse.htm
- http://csep10.phys.utk.edu/astr161/lect/history/kepler.html
- http://www.lessonpaths.com/learn/i/unit-m-conic-section-applets/ellipse-drawn-from-definition-geogebra-dynamic-worksheet
- http://www.lessonpaths.com/learn/i/unit-m-conic-sections-in-real-life/conic-sections-in-real-life
No comments:
Post a Comment